What’s a triangular number? It is the sequence found by summing all the natural numbers, for example the third number is $1+2+3=6$. Interestingly, it counts objects arranged as a triangle.
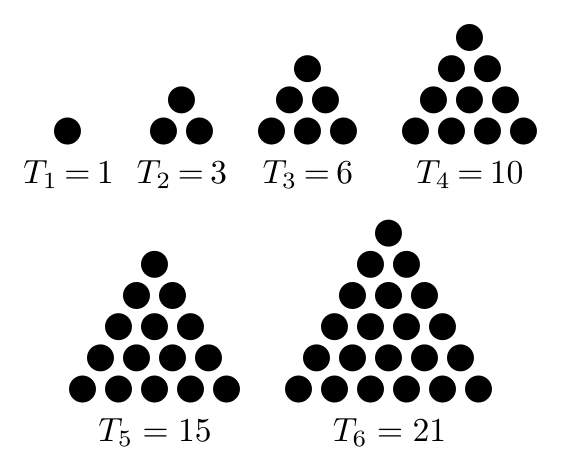
This also has closed form $T_n=\sum_{i=1}^{n}i=\frac{n(n+1)}{2}$.
I started with a brute force approach – iterate through the triangular numbers and test if the number of divisors is greater than 500. I’m using the “numbers” package’s Sigma function to implement divisor function $\sigma x(n)=\sum{d n}d^x$ where $\sigma _0(n)$ gives the total number of factors for a given number. That requires a loop, which is going to dominate for large $n$, so $O(n^2)$.
library(numbers)
triangular.number <- function(number) {
number = (number * (number + 1)) / 2
}
num.factors <- 0
i <- 1
while (num.factors < 500) {
num.factors <- (Sigma((triangular.number(i)), k = 0))
print(triangular.number(i)) i <- i + 1
}
Not terribly efficient but it gets the correct answer. So how can we improve the algorithm? Reducing the number of times we repeat the loop would be a good place to start.
Now, $a(n)$ and $b(n+1)$ are co-prime – the only positive integer that divides them both is 1. This has a useful property, that $lcm(a,b)=ab$. Thing is, I can’t see how to incorporate it…

Leave a Reply